How To Find The Distance Of A Circle

Shortest Distance between a Bespeak and a Circle

What is the distance between a circle $C$ with equation ${\mathrm{10}}^2+y^2=r^2$ which is centered at the origin and a point $P\left(x_1,y_1\right)$ ?

The ray $\overrightarrow{OP}$ , starting at the origin $O$ and passing through the indicate $P$ , intersects the circle at the point closest to $P$ . And so, the altitude between the circle and the bespeak will be the departure of the altitude of the point from the origin and the radius of the circumvolve.

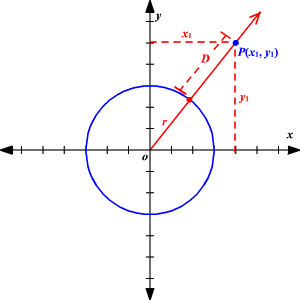
Using the Distance Formula , the shortest distance betwixt the point and the circle is $\left|\sqrt{{\left(x_1\right)}^{\mathrm{ii}}+{\left(y_1\right)}^2}-r\right|$ .

Notation that the formula works whether $P$ is within or outside the circumvolve.

If the circle is not centered at the origin simply has a eye say $\left(h,k\right)$ and a radius $r$ , the shortest distance between the indicate $P\left(x_1,y_{\mathrm{one}}\right)$ and the circle is $\left|\sqrt{{\left({\mathrm{10}}_1-h\right)}^2+{\left(y_1-k\right)}^2}-r\right|$ .

Case i:

What is the shortest distance between the circle $x^2+y^{\mathrm{ii}}=\mathrm{nine}$ and the point $A(3,4)$ ?

The circle is centered at the origin and has a radius $\mathrm{iii}$ .

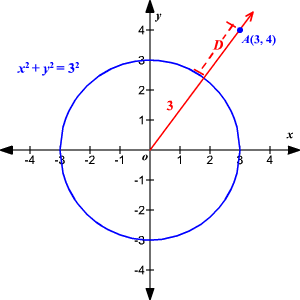
Then, the shortest distance $D$ between the point and the circle is given by

$\begin{array}{l}D=\left|\sqrt{{\left(\mathrm{iii}\right)}^2+{\left(4\right)}^2}-3\right|\\ =\left|\sqrt{25}-3\right|\\ =\left|5-3\right|\\ =\mathrm{two}\end{array}$

That is, the shortest distance between them is $2$ units.

Example 2:

What is the shortest distance between the circle $x^2+y^{\mathrm{ii}}=36$ and the point $Q(-2,2)$ ?

The circle is centered at the origin and has a radius $6$ .

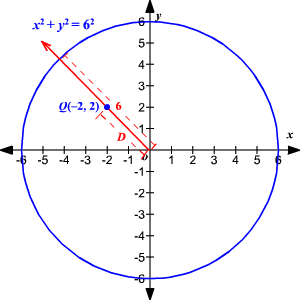
So, the shortest distance $D$ between the point and the circle is given by

$\begin{array}{l}D=\left|\sqrt{{(-2)}^2+{\left(\mathrm{ii}\right)}^2}-\mathrm{half-dozen}\right|\\ =\left|\sqrt{\mathrm{viii}}-\mathrm{half\; dozen}\right|\\ =\mathrm{half-dozen}-\mathrm{two}\sqrt{2}\\ \approx 3.17\end{array}$

That is, the shortest altitude between them is about $\mathrm{iii.17}$ units.

Example 3:

What is the shortest distance between the circle ${\left(x+3\right)}^2+{\left(y-3\right)}^2=5^2$ and the point $Z(-\mathrm{two},0)$ ?

Compare the given equation with the standard grade of equation of the circle,

${\left(\mathrm{ten}-h\right)}^2+{\left(y-k\right)}^{\mathrm{ii}}=r^{\mathrm{two}}$ where $(h,k)$ is the center and $r$ is the radius.

The given circumvolve has its heart at

$(-\mathrm{three},3)$

and has a radius of

$5$

units.

So, the shortest distance $D$ between the point and the circumvolve is given by

$\begin{array}{l}D=\left|\mathrm{five}-\sqrt{{\left(-3-\left(-2\right)\right)}^2+{\left(\mathrm{three}-0\right)}^{\mathrm{two}}}\right|\\ =\left|5-\sqrt{1+9}\right|\\ =\left|5-\sqrt{\mathrm{x}}\right|\\ \approx 1.84\end{array}$

That is, the shortest distance between them is virtually $\mathrm{one.84}$ units.

Instance 4:

What is the shortest altitude between the circle $x^2+y^{\mathrm{ii}}-\mathrm{eight}\mathrm{10}+10y-8=0$ and the point $P\left(-4,-\mathrm{xi}\right)$ ?

Rewrite the equation of the circle in the grade ${\left(x-h\right)}^2+{\left(y-\mathrm{grand}\right)}^2=r^2$ where $(h,g)$ is the center and $r$ is the radius.

$\begin{array}{l}{x}^2+y^{\mathrm{ii}}-\mathrm{eight}x+10y-\mathrm{viii}=0\\ x^2-\mathrm{viii}x+\mathrm{xvi}+y^{\mathrm{two}}+10y+25=8+16+25\\ {\left(x-\mathrm{iv}\right)}^2+{\left(y+5\right)}^{\mathrm{two}}=49\\ {\left(x-\mathrm{iv}\right)}^{\mathrm{two}}+{\left(y+\mathrm{five}\right)}^2=7^2\end{array}$

And so, the circle has its center at

$(\mathrm{iv},-5)$

and has a radius of

$\mathrm{seven}$

units.

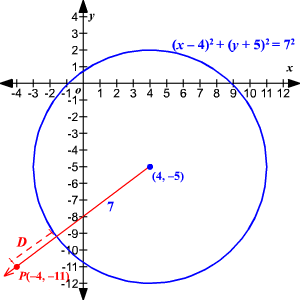
Then, the shortest distance $D$ between the point and the circle is given by

$\begin{array}{c}D=\left|\sqrt{{\left(-4-\mathrm{four}\right)}^{\mathrm{two}}+{\left(-11-\left(-5\right)\right)}^{\mathrm{two}}}-\mathrm{vii}\right|\\ =\left|\sqrt{64+36}-7\right|\\ =\sqrt{100}-7\\ =3\end{array}$

That is, the shortest altitude between them is $3$ units.

Source: https://www.varsitytutors.com/hotmath/hotmath_help/topics/shortest-distance-between-a-point-and-a-circle

Posted by: fieldsforomed.blogspot.com

Share this post